Voltage divider rule finds the voltage over a load in electrical circuit, when the loads are connected in series.
For a DC circuit with constant voltage source VT and resistors in series, the voltage drop Vi in resistor Ri is given by the formula:
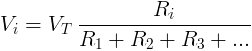
Vi - voltage drop in resistor Ri in volts [V].
VT - the equivalent voltage source or voltage drop in volts [V].
Ri - resistance of resistor Ri in ohms [Ω].
R1 - resistance of resistor R1 in ohms [Ω].
R2 - resistance of resistor R2 in ohms [Ω].
R3 - resistance of resistor R3 in ohms [Ω].
Voltage source of VT=30V is connected to resistors in series, R1=30Ω, R2=40Ω.
Find the voltage drop on resistor R2.
V2 = VT × R2 / (R1+R2) = 30V × 40Ω / (30Ω+40Ω) = 17.14V
For an AC circuit with voltage source VT and loads in series, the voltage drop Vi in load Zi is given by the formula:
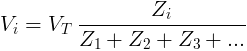
Vi - voltage drop in load Zi in volts [V].
VT - the equivalent voltage source or voltage drop in volts [V].
Zi - impedance of load Zi in ohms [Ω].
Z1 - impedance of load Z1 in ohms [Ω].
Z2 - impedance of load Z2 in ohms [Ω].
Z3 - impedance of load Z3 in ohms [Ω].
Voltage source of VT=30V∟60° is connected to loads in series, Z1=30Ω∟20°, Z2=40Ω∟-50°.
Find the voltage drop in load Z1.
V2 = VT × Z1 / (Z1+Z2)
= 30V∟60° × 30Ω∟20° / (30Ω∟20°+40Ω∟-50°)
= 30V∟60° × 30Ω∟20° / (30cos(20)+j30sin(20)+40cos(-50)+j40sin(-50))
= 30V∟60° × 30Ω∟20° / (28.19+j10.26+25.71-j30.64)
= 30V∟60° × 30Ω∟20° / (53.9-j20.38)
= 30V∟60° × 30Ω∟20° / 57.62Ω∟-20.71°
= (30V×30Ω/57.62Ω) ∟ (60°+20°+20.71°)
= 15.62V∟100.71°