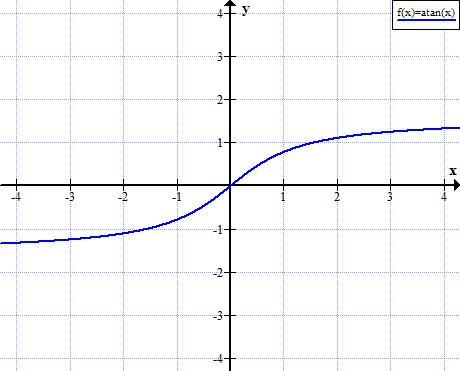
Arctan(x), tan-1(x), inverse tangent function.
The arctangent of x is defined as the inverse tangent function of x when x is real (x∈ℝ).
When the tangent of y is equal to x:
tan y = x
Then the arctangent of x is equal to the inverse tangent function of x, which is equal to y:
arctan x= tan-1 x = y
arctan 1 = tan-1 1 = π/4 rad = 45°
| Rule name | Rule |
|---|---|
| Tangent of arctangent |
tan( arctan x ) = x |
| Arctan of negative argument |
arctan(-x) = - arctan x |
| Arctan sum |
arctan α + arctan β = arctan [(α+β) / (1-αβ)] |
| Arctan difference |
arctan α - arctan β = arctan [(α-β) / (1+αβ)] |
| Sine of arctangent |
|
| Cosine of arctangent |
|
| Reciprocal argument |
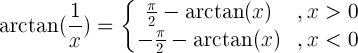 |
| Arctan from arcsin |
|
| Derivative of arctan |
|
| Indefinite integral of arctan |
|
| x | arctan(x) (rad) |
arctan(x) (°) |
|---|---|---|
| -∞ | -π/2 | -90° |
| -3 | -1.2490 | -71.565° |
| -2 | -1.1071 | -63.435° |
| -√3 | -π/3 | -60° |
| -1 | -π/4 | -45° |
| -1/√3 | -π/6 | -30° |
| -0.5 | -0.4636 | -26.565° |
| 0 | 0 | 0° |
| 0.5 | 0.4636 | 26.565° |
| 1/√3 | π/6 | 30° |
| 1 | π/4 | 45° |
| √3 | π/3 | 60° |
| 2 | 1.1071 | 63.435° |
| 3 | 1.2490 | 71.565° |
| ∞ | π/2 | 90° |