Probability Distribution

In probability and statistics distribution is a characteristic of a random variable, describes the probability of the random variable in each value.

Each distribution has a certain probability density function and probability distribution function.

Though there are indefinite number of probability distributions, there are several common distributions in use.

Cumulative distribution function

The probability distribution is described by the cumulative distribution function F(x),

which is the probability of random variable X to get value smaller than or equal to x:

F(x) = P(X ≤ x)

Continuous distribution

The cumulative distribution function F(x) is calculated by integration of the probability density function f(u) of continuous random variable X.

Discrete distribution

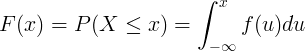
The cumulative distribution function F(x) is calculated by summation of the probability mass function P(u) of discrete random variable X.

Continuous distributions table

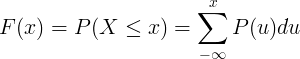
Continuous distribution is the distribution of a continuous random variable.

Continuous distribution example

...

Continuous distributions table

Distribution name Distribution symbol Probability density function (pdf) Mean Variance
   

fX(x)

μ = E(X)

σ2 = Var(X)
Normal / gaussian

X ~ N(μ,σ2)

 \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} μ σ 2
Uniform

X ~ U(a,b)

 \begin{Bmatrix}\frac{1}{b-a} & ,a\leq x\leq b\\ & \\0 & ,otherwise\end{matrix} \frac{(b-a)^2}{12}
Exponential X ~ exp(λ) \begin{Bmatrix}\lambda e^{-\lambda x} & x\geq 0\\ 0 & x<0\end{matrix} \frac{1}{\lambda} \frac{1}{\lambda^2}
Gamma X ~ gamma(c, λ) \frac{\lambda ^c x^{c-1}e^{-\lambda x}}{\Gamma (c)}

x > 0, c > 0, λ > 0

 \frac{c}{\lambda } \frac{c}{\lambda ^2}
Chi square

X ~ χ 2(k)

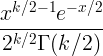 \frac{x^{k/2-1}e^{-x/2}}{2^{k/2}\Gamma (k/2)}

k

2k
Wishart        
F

X ~ F (k1, k2)

      
Beta        
Weibull        
Log-normal

X ~ LN(μ,σ2)

      
Rayleigh        
Cauchy        
Dirichlet        
Laplace        
Levy        
Rice        
Student's t        

Discrete distributions table

Discrete distribution is the distribution of a discrete random variable.

Discrete distribution example

...

Discrete distributions table

Distribution name Distribution symbol Probability mass function (pmf) Mean Variance
    fx(k) = P(X=k)

k = 0,1,2,...

 E(x) Var(x)
Binomial

X ~ Bin(n,p)

 \binom{n}{k}p^{k}(1-p)^{n-k}

np

np(1-p)
Poisson

X ~ Poisson(λ)

λ ≥ 0

λ

λ
Uniform

X ~ U(a,b)

 \begin{Bmatrix}\frac{1}{b-a+1} & ,a\leq k\leq b\\ & \\0 & ,otherwise\end{matrix} \frac{a+b}{2} \frac{(b-a+1)^{2}-1}{12}
Geometric

X ~ Geom(p)

 p(1-p)^{k}

\frac{1-p}{p}

\frac{1-p}{p^2}
Hyper-geometric

X ~ HG(N,K,n)

N = 0,1,2,...

K = 0,1,..,N

n = 0,1,...,N

 \frac{nK}{N} \frac{nK(N-K)(N-n)}{N^2(N-1)}
Bernoulli

X ~ Bern(p)

 \begin{Bmatrix}(1-p) & ,k=0\\ p & ,k=1\\ 0 & ,otherwise\end{matrix}

p

p(1-p)

 

See also

Write how to improve this page

PROBABILITY & STATISTICS
RAPID TABLES